前言

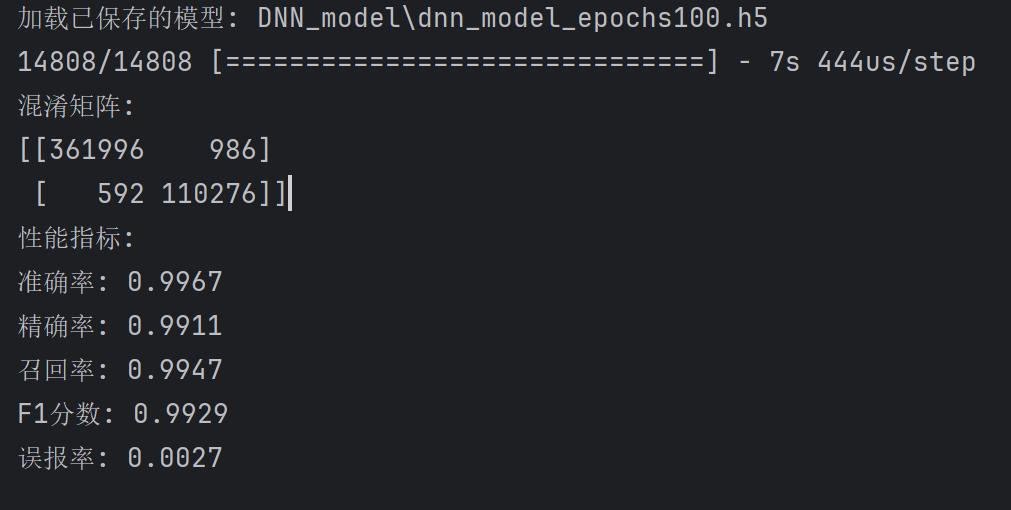
在昨天的AE+DNN基础上加上了GSmote，套成了整个完整模型，最终分类效果还不错，最好的一次效果如下：

准确率: 0.9967
精确率: 0.9911
召回率: 0.9947
F1分数: 0.9929
误报率: 0.0027

最好的模型已经保存下来了，AE的模型为AE_model_15_epochs50_bs128.h5,DNN的模型为dnn_model_epochs100.h5

实验参数

GeometricSMOTE

target_counts

"DoS GoldenEye": 20000,
"FTP-Patator": 20000,
"SSH-Patator": 20000,
"DoS slowloris": 20000,
"DoS Slowhttptest": 20000,
"Bot": 20000,

GeometricSMOTE初始化参数

random_state = 42
k_neighbors=5
selection_strategy=’combined’
sampling_strategy=target_counts

DNN

DNN模型结构

# 构建 DNN 模型
model = tf.keras.Sequential([
    tf.keras.layers.InputLayer(input_shape=(X_train_scaled.shape[1],)),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(64, activation='relu'),
    tf.keras.layers.Dense(32, activation='relu'),
    tf.keras.layers.Dense(1, activation='sigmoid')  # 输出层为二分类
])

DNN训练参数

epochs=30
batch_size=128
validation_split=0.2
阈值=0.5

AE

encoder和decoder

# 编码器部分（多层）
encoded = tf.keras.layers.Dense(256, activation='relu')(input_layer)
encoded = tf.keras.layers.Dense(128, activation='relu')(encoded)
encoded = tf.keras.layers.Dense(64, activation='relu')(encoded)
encoded = tf.keras.layers.Dense(32, activation='relu')(encoded)
encoded = tf.keras.layers.Dense(encoding_dim, activation='relu')(encoded)

# 解码器部分（对称结构，多层）
decoded = tf.keras.layers.Dense(32, activation='relu')(encoded)
decoded = tf.keras.layers.Dense(64, activation='relu')(decoded)
decoded = tf.keras.layers.Dense(128, activation='relu')(decoded)
decoded = tf.keras.layers.Dense(256, activation='relu')(decoded)
decoded = tf.keras.layers.Dense(input_dim, activation='sigmoid')(decoded)

AE训练参数

epochs=20
batch_size=256
shuffle=True
validation_data=(X_test_scaled, X_test_scaled))
encoding_dim = 15  (输出维度)

实验结果

参数	指标	混淆矩阵
基准实验参数	准确率: 0.9908 精确率: 0.9750 召回率: 0.9860 F1分数: 0.9805 误报率: 0.0077	[[360179 2803] [ 1554 109314]]
同上，重复实验	准确率: 0.9947 精确率: 0.9820 召回率: 0.9954 F1分数: 0.9887 误报率: 0.0056	[[360963 2019] [ 507 110361]]
阈值=0.6	准确率: 0.9901 精确率: 0.9936 召回率: 0.9638 F1分数: 0.9785 误报率: 0.0019	[[362299 683] [ 4015 106853]]
同上，重复实验	准确率: 0.9955 精确率: 0.9886 召回率: 0.9921 F1分数: 0.9904 误报率: 0.0035	[[361716 1266] [ 877 109991]]
同上，重复实验使用训练后保存的AE模型	准确率: 0.9956 精确率: 0.9880 召回率: 0.9935 F1分数: 0.9907 误报率: 0.0037	[[361641 1341] [ 725 110143]]
同上，重复实验，保存DNN模型	准确率: 0.9937 精确率: 0.9848 召回率: 0.9883 F1分数: 0.9866 误报率: 0.0047	[[361294 1688] [ 1298 109570]]
使用保存的两个模型进行预测	准确率: 0.9937 精确率: 0.9848 召回率: 0.9883 F1分数: 0.9866 误报率: 0.0047	[[361294 1688] [ 1298 109570]]
同上，重复实验	准确率: 0.9937 精确率: 0.9848 召回率: 0.9883 F1分数: 0.9866 误报率: 0.0047	[[361294 1688] [ 1298 109570]]
可以看出如果用的是同一个模型	预测的结果也是相同的	不会发生变化
阈值改为0.7	准确率: 0.9931 精确率: 0.9875 召回率: 0.9831 F1分数: 0.9853 误报率: 0.0038	[[361606 1376] [ 1871 108997]]
跟上面的结果一样	准确率: 0.9931 精确率: 0.9875 召回率: 0.9831 F1分数: 0.9853 误报率: 0.0038	[[361606 1376] [ 1871 108997]]
阈值改为0.5	准确率: 0.9937 精确率: 0.9828 召回率: 0.9904 F1分数: 0.9866 误报率: 0.0053	[[361065 1917] [ 1064 109804]]
还真的是不变	准确率: 0.9937 精确率: 0.9828 召回率: 0.9904 F1分数: 0.9866 误报率: 0.0053	[[361065 1917] [ 1064 109804]]
阈值改为0.9	准确率: 0.9878 精确率: 0.9990 召回率: 0.9487 F1分数: 0.9732 误报率: 0.0003	[[362879 103] [ 5687 105181]]
同上	准确率: 0.9878 精确率: 0.9990 召回率: 0.9487 F1分数: 0.9732 误报率: 0.0003	[[362879 103] [ 5687 105181]]
阈值为0.5 DNN训练100轮，batch_size=128 AE训练50轮,batch_size=128 已保存模型 GSmote的k_neighbors=4 生成样本数量全部改成为30000	准确率: 0.9967 精确率: 0.9911 召回率: 0.9947 F1分数: 0.9929 误报率: 0.0027	[[361996 986] [ 592 110276]]
训练集和测试集以7:3的比例划分，使用训练好的AE和DNN模型进行训练	准确率: 0.9966 精确率: 0.9911 召回率: 0.9945 F1分数: 0.9928 误报率: 0.0027	[[542987 1486] [ 913 165389]]

截止当前最好的一次GSmote+AE+DNN实验结果

存在问题

使用保存好的AE和DNN模型来进行预测时，每次预测结果都是一样的！！，多次运行代码，只要是使用保存下来的同一个模型，那么每次运行的结果都是一样的，包括准确率、精确率、召回率、F1分数、误报率、混淆矩阵都是一样的，一个小数点都没变，具体可以看上面的实验结果表格。但是如果更换了训练集和测试集的比例(例如换到7:3)，虽然最后出来的混淆矩阵样本数量不一样,但是各种评估指标还是十分相近的，变数在小数点后三位，前两位的0.99xx都是不变的，误差大概只有0.0001，数量不一样，但是比例是将近一模一样的。

不知道这样子到底符不符合流程，毕竟每一次使用保存的模型来预测真的是一个样本误差都没有！！以我的看法应该是每一次预测都应该会存在一定细小的误差，可以不大，但是应该有改变才对呀。

如果每一次都从头训练的话，那预测出来的结果每次都不太一样，有细微的误差，但是这个太耗时间了，每次训练预测都要十分钟左右。这种做法应该是比较正确的，世间难得两全法，当前还是采用保存模型的方法先吧。

补充

如果改变分割训练集和测试集的随机种子random_state，再使用之前保存好的模型进行预测，会不会产生不一样的结果呢？猜想的结果是每使用一个随机种子，再使用保存下来的AE+DNN模型进行预测，最后结果可能会产生细微的差别，但是不会影响大体结果，都在99%左右，仅仅是猜想，还没实践过。

1	X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state=42)

修改分割数据集的random_state

**结论:**修改random_state确实能让最终预测结果不一样。但是只是在不同random_state下产生不同的评估指标和混淆矩阵，如果使用保存好的AE+DNN模型来预测同一个random_state，那跟上面一样无论预测多少次最终结果都相同。

简而言之，不同random_state参数产生不同的预测结果，且最终结果相近，误差在1%，相同的random_state预测多轮每一次的结果都相同。

不同random_state实验结果

实验参数	评估指标	混淆矩阵
random_state=42	准确率: 0.9967 精确率: 0.9911 召回率: 0.9947 F1分数: 0.9929 误报率: 0.0027	[[361996 986] [ 592 110276]]
random_state=41 训练集测试集比例=8:2	准确率: 0.9840 精确率: 0.9940 召回率: 0.9370 F1分数: 0.9647 误报率: 0.0017	[[362360 622] [ 6980 103888]]
重复上面实验一样的结果	准确率: 0.9840 精确率: 0.9940 召回率: 0.9370 F1分数: 0.9647 误报率: 0.0017	[[362360 622] [ 6980 103888]]
random_state=40 这个结果也蛮好	准确率: 0.9967 精确率: 0.9915 召回率: 0.9943 F1分数: 0.9929 误报率: 0.0026	[[362034 948] [ 637 110231]]